LRC circuit
Table of Contents
1. Introduction
LRC circuits are equivalent to mass-spring oscillation systems in terms of the differential equation generated. In other words, they are an example of a wave generator. First we introduce the LRC circuit without a voltage source. Later, another circuit diagram will include a possibly variable voltage source.
\documentclass{article} \usepackage{circuitikz} \begin{document} \begin{center} \begin{circuitikz} \draw (0,0) to[resistor, l=\mbox{$R$}] (0,12) to[inductor, l=\mbox{$L$}] (12,12) to[capacitor, l=\mbox{$C$}] (12,0) (12,0) -- (0,0) (6,0) -- (6,-3) to (6, -3) node[shape=ground]{}; \end{circuitikz} \end{center} \end{document}
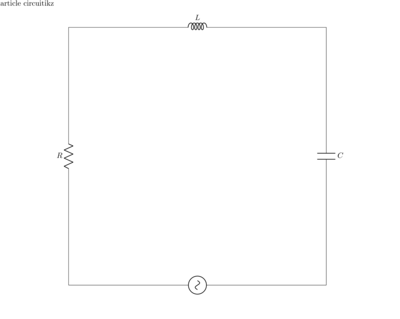
Figure 1: LRC Circuit without voltage source
2. Mass-Spring Equation Equivalence
We know these relations for the given circuit elements above:
\begin{align} v(t) = L\frac{di}{dt} \\ i(t) = C\frac{dv}{dt} \\ v = iR \end{align}if we analyze the current signal, Kirchhoff's voltage law tells us that the total voltage drop throughout this circuit is zero. We use the capacitor equation in integral form and sum the voltages:
\begin{align*} L\frac{di}{dt} + \frac{1}{C}\int i(t)dt + iR = 0 \end{align*}We then take a derivative to remove the integral:
\begin{align*} L\frac{d^{2}i}{dt^{2}} + R\frac{di}{dt} + \frac{1}{C}i = 0 \\ (LD^{2} + RD + \frac{1}{C}) i(t) = 0 \end{align*}it is clear that the characteristic polynomial of this homogeneous linear differential equation is:
\begin{align*} L\lambda^{2} + R\lambda + \frac{1}{C} = 0 \end{align*}which, utilizing the quadratic formula, has the solutions:
\begin{align*} \lambda_{1} = \frac{-R + \sqrt{R^{2} - \frac{4L}{C}}}{2L}, \lambda_{2} = \frac{-R - \sqrt{R^{2} - \frac{4L}{C}}}{2L} \end{align*}which implies the general solution to this differential equation is:
\begin{align*} i(t) = Ae^{\lambda_{1} t} + Be^{\lambda_{2} t} \end{align*}We can make this nicer by setting \(-\frac{R}{2L} = m\), \(\frac{\sqrt{R^{2} - \frac{4L}{C}}}{2L} = p\), then \(\lambda_{1} = m + p\), \(\lambda_{2} = m - p\). Then:
\begin{align*} i(t) = Ae^{(m + p) t} + Be^{(m - p) t} \end{align*}2.1. Underdampened Oscillation
In the case \(R^{2} < \frac{4L}{C}\), \(p = i\frac{\sqrt{\sigma}}{2L}\) for some \(\sigma > 0\). We re-cast \(\lambda = \frac{\sqrt{\sigma}}{2L}\) so \(p = i\lambda\). Then:
\begin{align*} i(t) = Ae^{m + i\lambda t} + Be^{m -i\lambda t} \end{align*}This function \(i(t)\) clearly describes an sinusoidal oscillation.
2.2. Critical Oscillation
In the case \(R^{2} - \frac{4L}{C} = 0\), we have:
\begin{align*} i(t) = Ae^{mt} + Be^{mt} = Ce^{mt} \end{align*}note that this is actually a decaying solution because \(m\) must be negative.
3. AC Voltage Source
Here is the circuit diagram for the LRC circuit with a voltage source:
\documentclass{article} \usepackage{circuitikz} \begin{document} \begin{center} \begin{circuitikz} \draw (0,0) to[resistor, l=\mbox{$R$}] (0,12) to[inductor, l=\mbox{$L$}] (12,12) to[capacitor, l=\mbox{$C$}] (12,0) (12,0) to[sinusoidal voltage source] (0,0); \end{circuitikz} \end{center} \end{document}
 This new differential equation looks like this:
This new differential equation looks like this:
where the right hand side of the equation includes the term created by the AC voltage source. Now we take the Laplace Transform of both sides (using euler notation to keep track of the phase shift \(\phi\)):
\begin{align} \label{} \mathcal{L}\{LD^{2} + RD + \frac{1}{C}\}i(t) = V_{0}e^{i\phi}\mathcal{L}\{e^{i 2\pi\omega t}\} \\ L(s^{2}I(s) - s i(0) - i'(0)) + R(sI(s) - i(0)) + \frac{1}{C}I(s) = V_{0}e^{i\phi}\mathcal{L}\{e^{i 2\pi\omega t}\} \\ (Ls^{2} + (R - i(0))s + \frac{1}{C})I(s) = V_{0}e^{i\phi}\mathcal{L}\{e^{i 2\pi\omega t}\} + i'(0) + i(0) \\ I(s) = \frac{V_{0}e^{i\phi}\frac{1}{s - 2\pi i \omega} + i'(0) + i(0)}{Ls^{2} + (R - i(0))s + \frac{1}{C}} \\ i(t) = \mathcal{L}^{-1}\{\frac{V_{0}e^{i\phi}}{(s - 2\pi i \omega)(Ls^{2} + (R - i(0))s + \frac{1}{C})}\} + \mathcal{L}^{-1}\{\frac{i'(0) + i(0)}{Ls^{2} + (R - i(0))s + \frac{1}{C}}\} \end{align}We want to use partial fraction decomposition in order to break these denominators apart, so that doing the inverse transform is easier (the Laplace transform is linear). Now we already know the roots of the polynomial, and we can set the root \(2\pi i\omega = z_{1}\). Let's also ignore the rightmost term for now:
\begin{align} \label{Pain} i(t) = V_{0}e^{i\phi}\mathcal{L}^{-1}\{\frac{1}{(s - z_{1})(s - z_{2})(s - z_{3})}\} \end{align}where \(z_{2}\) and \(z_{3}\) are the two roots we found for the homogeneous case. We then use partial fraction decomposition:
\begin{align} \label{} \frac{1}{(s - z_{1})(s - z_{2})(s - z_{3})} = \frac{A}{s - z_{1}} + \frac{B}{s - z_{2}} + \frac{C}{s - z_{3}} \\ A(s - z_{2})(s - z_{3}) + B(s - z_{1})(s - z_{3}) + C(s - z_{1})(s - z_{2}) = 1 \end{align}from this we know:
\begin{align} \label{} A + B + C = 0 \\ z_{2}z_{3}A + z_{1}z_{3}B + z_{1}z_{2}C = 1 \\ (z_{2} + z_{3})A + (z_{1} + z_{3})B + (z_{1} + z_{2})C = 0 \end{align}Which is a linear system of equations. Eliminating C:
\begin{align} \label{} (z_{2}z_{3} - z_{1}z_{2})A + (z_{1}z_{3} - z_{1}z_{2})B = 1 \\ (z_{2} + z_{3})A + (z_{1} + z_{3})B - (z_{1} + z_{2})(A + B) = 0 \end{align}Now we want to eliminate B:
\begin{align} \label{} [(z_{2} + z_{3}) - (z_{1} + z_{2})]A + [(z_{1} + z_{3}) - (z_{1} + z_{2})]B = 0 \\ (z_{3} - z_{1})A + (z_{3} - z_{2})B = 0 \\ B = -\frac{z_{3} - z_{1}}{z_{3} - z_{2}}A \\ \end{align}finally, we have one equation in terms of A:
\begin{align} \label{} [(z_{2}z_{3} - z_{1}z_{2}) - (z_{1}z_{3} - z_{1}z_{2})\frac{z_{3} - z_{1}}{z_{3} - z_{2}}]A = 1 \\ [(z_{2}z_{3} - z_{1}z_{2})\frac{z_{3} - z_{2}}{z_{3} - z_{2}} - (z_{1}z_{3} - z_{1}z_{2})\frac{z_{3} - z_{1}}{z_{3} - z_{2}}]A = 1 \\ \frac{(z_{2}z_{3} - z_{1}z_{2})(z_{3} - z_{2}) - (z_{1}z_{3} - z_{1}z_{2})(z_{3} - z_{1})}{z_{3} - z_{2}}A = 1 \\ \frac{z_{2}z_{3}^{2} - z_{1}z_{2}z_{3} - z_{2}^{2}z_{3} + z_{1}z_{2}^{2} - z_{1}z_{3}^{2} + z_{1}z_{2}z_{3} + z_{1}^{2}z_{3} - z_{1}^{2}z_{2}}{z_{3} - z_{2}}A = 1 \\ \frac{z_{2}z_{3}^{2} - z_{2}^{2}z_{3} + z_{1}z_{2}^{2} - z_{1}z_{3}^{2} + z_{1}^{2}z_{3} - z_{1}^{2}z_{2}}{z_{3} - z_{2}}A = 1 \\ A = \frac{z_{3} - z_{2}}{z_{2}z_{3}^{2} + z_{1}z_{2}^{2} + z_{1}^{2}z_{3} - z_{1}z_{3}^{2} - z_{1}^{2}z_{2} - z_{2}^{2}z_{3}} \\ B = -\frac{z_{3} - z_{1}}{z_{3} - z_{2}}A \\ B = -\frac{z_{3} - z_{1}}{z_{2}z_{3}^{2} + z_{1}z_{2}^{2} + z_{1}^{2}z_{3} - z_{1}z_{3}^{2} - z_{1}^{2}z_{2} - z_{2}^{2}z_{3}} \\ C = -(A + B) \\ C = \frac{z_{2} - z_{1}}{z_{2}z_{3}^{2} + z_{1}z_{2}^{2} + z_{1}^{2}z_{3} - z_{1}z_{3}^{2} - z_{1}^{2}z_{2} - z_{2}^{2}z_{3}} \end{align}So we have the three coefficients:
\begin{align} \label{} A = \frac{z_{3} - z_{2}}{z_{2}z_{3}^{2} + z_{1}z_{2}^{2} + z_{1}^{2}z_{3} - z_{1}z_{3}^{2} - z_{1}^{2}z_{2} - z_{2}^{2}z_{3}} \\ B = \frac{z_{1} - z_{3}}{z_{2}z_{3}^{2} + z_{1}z_{2}^{2} + z_{1}^{2}z_{3} - z_{1}z_{3}^{2} - z_{1}^{2}z_{2} - z_{2}^{2}z_{3}} \\ C = \frac{z_{2} - z_{1}}{z_{2}z_{3}^{2} + z_{1}z_{2}^{2} + z_{1}^{2}z_{3} - z_{1}z_{3}^{2} - z_{1}^{2}z_{2} - z_{2}^{2}z_{3}} \end{align}The resulting solution looks like this:
\begin{align} \label{} i(t) = V_{0}e^{i\phi}(Ae^{z_{1}t} + Be^{z_{2}t} + Ce^{z_{3}t}) \end{align}where:
\begin{align} \label{} z_{1} = 2\pi i \omega \\ z_{2} = \frac{-(R - i(0)) + \sqrt{(R - i(0))^{2} - \frac{4L}{C}}}{2L} \\ z_{3} = \frac{-(R - i(0)) - \sqrt{(R - i(0))^{2} - \frac{4L}{C}}}{2L} \end{align}by taking the inverse Laplace Transform. The other terms can be either ignored if \(i'(0) = 0\) and \(i(0) = 0\) or one can solve for them in the same way. Solving for the two other terms:
\begin{align} \label{} \frac{1}{(s - z_{2})(s - z_{3})} = \frac{D}{s - z_{2}} + \frac{E}{s - z_{3}} \\ D(s - z_{3}) + E(s - z_{2}) = 1 \\ D + E = 0 \\ D z_{3} + E z_{2} = -1 \end{align}We have a much easier linear system:
\begin{align} \label{} E = -D \\ D(z_{3} - z_{2}) = -1 \\ D = -\frac{1}{z_{3} - z_{2}} \\ E = \frac{1}{z_{3} - z_{2}} \end{align}so the full solution including the terms used for the initial value problem looks like this:
\begin{align} \label{} i(t) = V_{0}e^{i\phi}(Ae^{z_{1}t} + Be^{z_{2}t} + Ce^{z_{3}t}) + (i'(0) + i(0))(De^{z_{2}t} + Ee^{z_{3}t}) \end{align}the sinusoidal part of the solution looks like this:
\begin{align} \label{hello world} \frac{(z_{3} - z_{2})V_{0}e^{i\phi}e^{2\pi i\omega t}}{z_{2}z_{3}^{2} + z_{1}z_{2}^{2} + z_{1}^{2}z_{3} - z_{1}z_{3}^{2} - z_{1}^{2}z_{2} - z_{2}^{2}z_{3}} \end{align}4. Mass-Spring System
Starting from Newtonian mechanics in a single dimension:
\begin{align} \label{} F_{net} = \sum_{i} m\frac{d^{2}x}{dt} \end{align}With Hooke's law:
\begin{align} \label{} F = -kx \end{align}then:
\begin{align} \label{} m\ddot{x} = -kx \\ m\ddot{x} + kx = 0 \end{align}We can define some damping force to be:
\begin{align} \label{} F_{damp} = -a\dot{x} \end{align}which will always resist a change in the direction of motion. Then, the new equation is:
\begin{align} \label{} m\ddot{x} + a\dot{x} + kx = 0 \end{align}which has the same form as the above LRC circuit equation. Now, any external driving force will appear on the right hand side.